Case Study: Finite State Automata
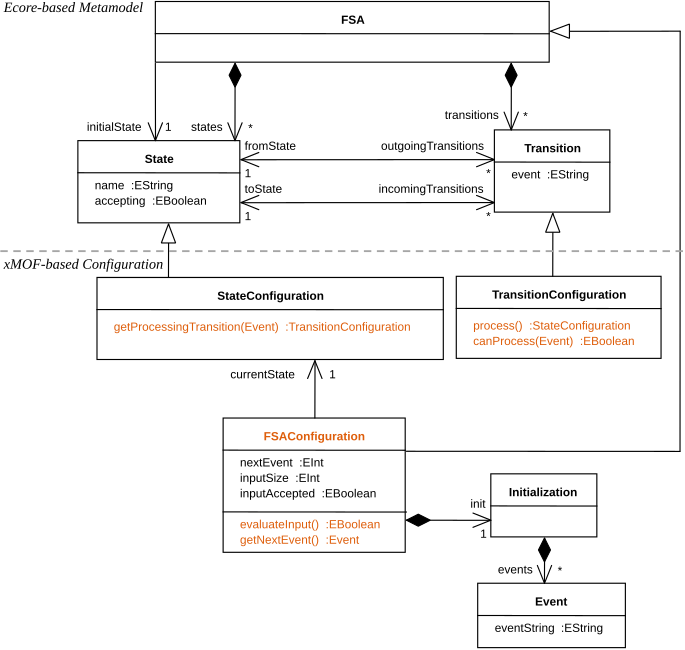
A Finite State Automata (FSA) processes a sequence of input symbols. In a given state, it checks if the next symbol matches any of the labels of the transitions that go out of a state. If the complete input sequence was processed and an accepting state was reached, the input sequence is valid.
The interesting aspects of this language is that its semantics specification defines that for executing an FSA model a sequence of input events (i.e., a sequence of input symbols) has to be additionally provided.
Example
This exemplary model of the FSA DSML (depicted in graphical concrete syntax) consists of a FSA containing three Statess1, s2, and s3, whereat s1 is the initial state of the automata and s3 is an accepting state. The Transitions of the automata process the input symbols “y”, “e”, and “s”. In the given example, the automata accepts input sequences of the form “y(e)*s” (i.e., “yes” with arbitrary many “e”).

Language Specification